6  Evaluate

The goal of syntheval is to make it simple to evaluate the utility and disclosure risk of synthetic data. It can be used with or without library(tidysynthesis).

6.1 Utility metrics

library(tidyverse)
library(syntheval)

theme_set(theme_minimal())

6.1.1 Setup

The following examples demonstrate utility and disclosure risk metrics using synthetic data based on the Palmer Penguins dataset (Horst, Hill, and Gorman 2020). library(syntheval) contains three built-in datasets:

  • penguins_conf: Pre-processed penguins data that were passed into the synthesizer.
  • penguins_postsynth: A postsynth object synthesized from penguins using library(tidysynthesis).
  • penguins_syn_df: A data frame pulled from penguins_postsynth. This is used to demonstrate how library(syntheval) works with output from a synthesizer different than library(tidysynthesis).

Functions like util_proportions() and util_moments() have different behaviors for postsynth objects and data frames. By default, they only show synthesized variables for postsynth objects and show all common variables for data frames. The common_vars and synth_vars arguments can change this behavior.

6.1.2 Proportions

util_proportions() compares the proportions of classes from categircal variables in the original and synthetic data.

util_proportions(
  postsynth = penguins_postsynth, 
  data = penguins_conf
)
# A tibble: 2 × 5
# Groups:   variable [1]
  variable class  synthetic original difference
  <chr>    <fct>      <dbl>    <dbl>      <dbl>
1 sex      female     0.529    0.495     0.0330
2 sex      male       0.471    0.505    -0.0330

All common variables are shown when using a data frame.

util_proportions(
  postsynth = penguins_syn_df, 
  data = penguins_conf
)
# A tibble: 8 × 5
# Groups:   variable [3]
  variable class     synthetic original difference
  <chr>    <fct>         <dbl>    <dbl>      <dbl>
1 island   Biscoe        0.465    0.489    -0.0240
2 island   Dream         0.414    0.369     0.0450
3 island   Torgersen     0.120    0.141    -0.0210
4 sex      female        0.529    0.495     0.0330
5 sex      male          0.471    0.505    -0.0330
6 species  Adelie        0.459    0.438     0.0210
7 species  Chinstrap     0.234    0.204     0.0300
8 species  Gentoo        0.306    0.357    -0.0511

6.1.3 Means and Totals

util_moments() compares the counts, means, standard deviations, skewness, and kurtoses of the original and synthetic data.

util_moments(
  postsynth = penguins_postsynth, 
  data = penguins_conf
)
# A tibble: 20 × 6
   variable        statistic original synthetic difference proportion_difference
   <fct>           <fct>        <dbl>     <dbl>      <dbl>                 <dbl>
 1 bill_length_mm  count      3.33e+2  333          0                    0      
 2 bill_length_mm  mean       4.40e+1   43.5       -0.502               -0.0114 
 3 bill_length_mm  sd         5.47e+0    5.54       0.0723               0.0132 
 4 bill_length_mm  skewness   4.51e-2    0.0646     0.0195               0.432  
 5 bill_length_mm  kurtosis  -8.88e-1   -0.948     -0.0598               0.0674 
 6 bill_depth_mm   count      3.33e+2  333          0                    0      
 7 bill_depth_mm   mean       1.72e+1   17.3        0.122                0.00712
 8 bill_depth_mm   sd         1.97e+0    1.89      -0.0762              -0.0387 
 9 bill_depth_mm   skewness  -1.49e-1   -0.278     -0.129                0.867  
10 bill_depth_mm   kurtosis  -8.97e-1   -0.742      0.155               -0.172  
11 flipper_length… count      3.33e+2  333          0                    0      
12 flipper_length… mean       2.01e+2  199.        -1.70                -0.00847
13 flipper_length… sd         1.40e+1   13.9       -0.135               -0.00961
14 flipper_length… skewness   3.59e-1    0.611      0.253                0.705  
15 flipper_length… kurtosis  -9.65e-1   -0.704      0.261               -0.270  
16 body_mass_g     count      3.33e+2  333          0                    0      
17 body_mass_g     mean       4.21e+3 4162.       -45.0                 -0.0107 
18 body_mass_g     sd         8.05e+2  783.       -22.3                 -0.0277 
19 body_mass_g     skewness   4.70e-1    0.655      0.185                0.394  
20 body_mass_g     kurtosis  -7.40e-1   -0.388      0.353               -0.477

util_totals() is similar to util_moments() but looks at counts and totals.

util_totals(
  postsynth = penguins_postsynth, 
  data = penguins_conf
)
# A tibble: 8 × 6
  variable         statistic original synthetic difference proportion_difference
  <fct>            <fct>        <dbl>     <dbl>      <dbl>                 <dbl>
1 bill_length_mm   count         333       333         0                 0      
2 bill_length_mm   total       14650.    14483.     -167.               -0.0114 
3 bill_depth_mm    count         333       333         0                 0      
4 bill_depth_mm    total        5716.     5757.       40.7               0.00712
5 flipper_length_… count         333       333         0                 0      
6 flipper_length_… total       66922     66355      -567                -0.00847
7 body_mass_g      count         333       333         0                 0      
8 body_mass_g      total     1400950   1385950    -15000                -0.0107

6.1.4 Percentiles

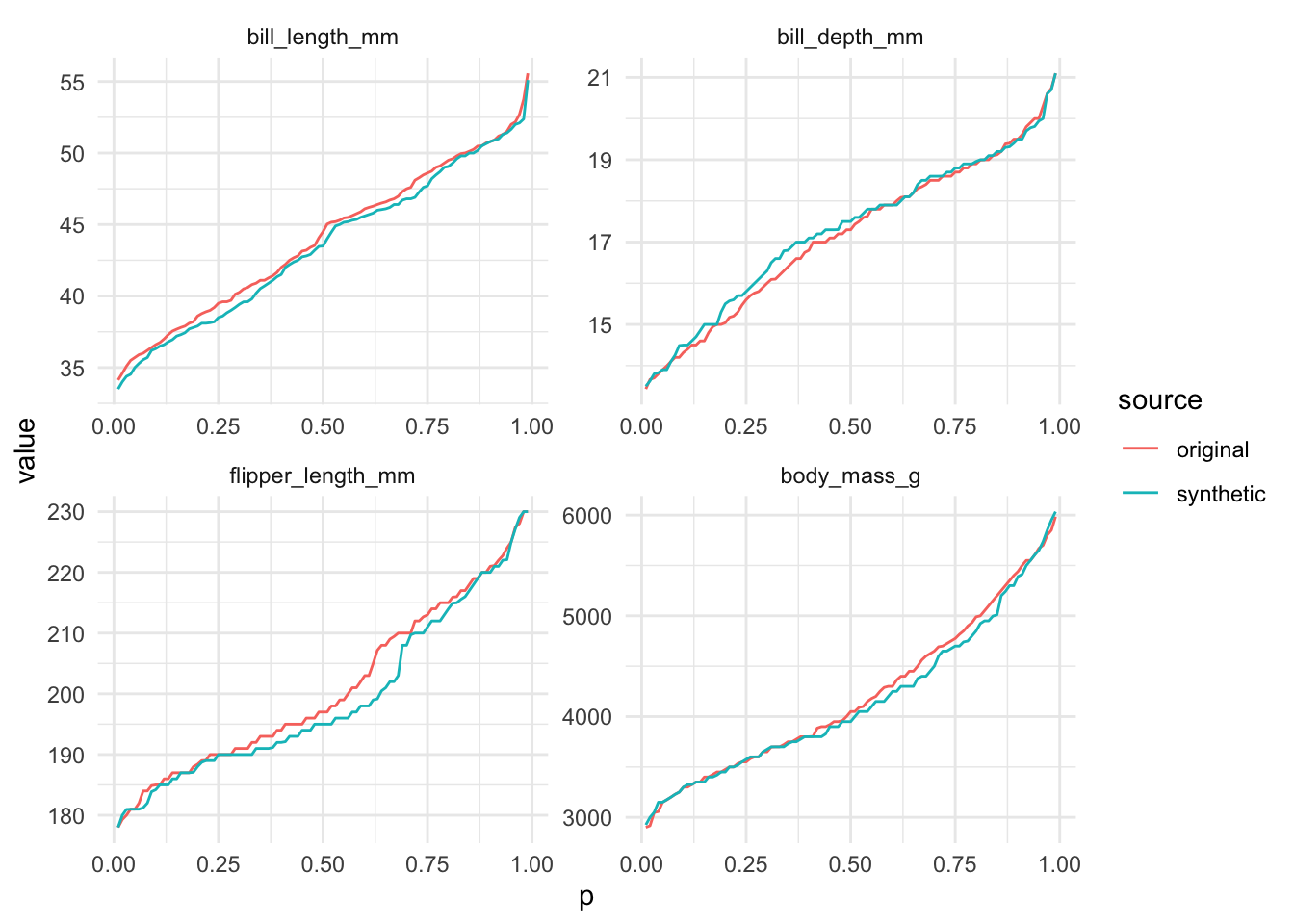
util_percentiles() compares percentiles from the original and synthetic data. The default percentiles are c(0.1, 0.5, 0.9) and can be easily overwritten.

util_percentiles(
  postsynth = penguins_postsynth, 
  data = penguins_conf,
  probs = c(0.5, 0.8)
)
# A tibble: 8 × 6
      p variable          original synthetic difference proportion_difference
  <dbl> <fct>                <dbl>     <dbl>      <dbl>                 <dbl>
1   0.5 bill_length_mm        44.5      43.5    -1                   -0.0225 
2   0.8 bill_length_mm        49.5      49.1    -0.440               -0.00889
3   0.5 bill_depth_mm         17.3      17.5     0.200                0.0116 
4   0.8 bill_depth_mm         18.9      19.0     0.0600               0.00317
5   0.5 flipper_length_mm    197       195      -2                   -0.0102 
6   0.8 flipper_length_mm    215       214      -1                   -0.00465
7   0.5 body_mass_g         4050      3950    -100                   -0.0247 
8   0.8 body_mass_g         4990      4850    -140                   -0.0281

The functions are designed to work well with library(ggplot2).

util_percentiles(
  postsynth = penguins_postsynth, 
  data = penguins_conf,
  probs = seq(0.01, 0.99, 0.01)
) |>
  pivot_longer(
    cols = c(original, synthetic),
    names_to = "source",
    values_to = "value"
  ) |>
  ggplot(aes(x = p, y = value, color = source)) +
  geom_line() +
  facet_wrap(~ variable, scales = "free")

6.1.5 KS Distance

util_ks_distance() shows the Kolmogorov-Smirnov distance between the original distribution and synthetic distribution for numeric variables. The function also returns the point(s) of the maximum distance.

util_ks_distance(
  postsynth = penguins_syn_df, 
  data = penguins_conf
)
# A tibble: 14 × 3
   variable           value      D
   <chr>              <dbl>  <dbl>
 1 bill_length_mm      38.7 0.0601
 2 bill_depth_mm       16.7 0.0511
 3 bill_depth_mm       16.7 0.0511
 4 bill_depth_mm       16.8 0.0511
 5 bill_depth_mm       16.8 0.0511
 6 flipper_length_mm  196.  0.0781
 7 flipper_length_mm  196.  0.0781
 8 flipper_length_mm  197.  0.0781
 9 flipper_length_mm  197.  0.0781
10 flipper_length_mm  197.  0.0781
11 body_mass_g       4359.  0.0480
12 body_mass_g       4370.  0.0480
13 body_mass_g       4381.  0.0480
14 body_mass_g       4392.  0.0480

6.1.6 Co-Occurrence

util_co_occurence() differences the lower triangles of co-occurrence matrices calculated on numeric variables in the original data and synthetic data.

co_occurrence <- util_co_occurrence(
  postsynth = penguins_postsynth, 
  data = penguins_conf
)

co_occurrence$co_occurrence_difference
                  bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
bill_length_mm                NA            NA                NA          NA
bill_depth_mm                  0            NA                NA          NA
flipper_length_mm              0             0                NA          NA
body_mass_g                    0             0                 0          NA

The function returns the MAE for co-occurrences, which provides a sense of the median error between the original and synthetic data. The function also returns the RMSE for co-occurrences, which provides a sense of the average error between the original data and synthetic data.

co_occurrence$co_occurrence_difference_mae
[1] 0
co_occurrence$co_occurrence_difference_rmse
[1] 0

All observations have non-zero bill_length_mm, bill_depth_mm, flipper_length_mm, and body_mass_g. util_co_occurrence() is most useful for economic variables like income and wealth where 0 is a common value.

6.1.7 Correlations

util_corr_fit() differences the lower triangles of correlation matrices calculated on numeric variables in the original data and synthetic data.

corr_fit <- util_corr_fit(
  postsynth = penguins_postsynth, 
  data = penguins_conf
)

round(corr_fit$correlation_difference, digits = 3)
                  bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
bill_length_mm                NA            NA                NA          NA
bill_depth_mm             -0.069            NA                NA          NA
flipper_length_mm         -0.003        -0.048                NA          NA
body_mass_g                0.031        -0.011             -0.08          NA

The function returns the MAE for correlation coefficients, which provides a sense of the median error between the original and synthetic data. The function also returns the RMSE for the correlation coefficients, which provides a sense of the average error between the original synthetic data.

corr_fit$correlation_difference_mae
[1] 0.04034565
corr_fit$correlation_difference_rmse
[1] 0.04922324

6.1.8 Confidence Interval Overlap

util_ci_overlap() compares a linear regression models estimated on the original data and synthetic data. formula specifies the functional form of the regression model.

ci_overlap <- util_ci_overlap(
  postsynth = penguins_postsynth, 
  data = penguins_conf,
  formula = body_mass_g ~ bill_length_mm  + sex
)

$ci_overlap() summarizes each coefficient including how much the confidence intervals overlap, if the signs match, and if the statistical significance matches.

ci_overlap$ci_overlap 
# A tibble: 3 × 8
  term    overlap coef_diff std_coef_diff sign_match significance_match ss_match
  <chr>     <dbl>     <dbl>         <dbl> <lgl>      <lgl>              <lgl>   
1 (Inter…   0.963   -27.8         -0.0978 TRUE       TRUE               TRUE    
2 bill_l…   0.965     0.917        0.138  TRUE       TRUE               TRUE    
3 sexmale   0.951   -14.0         -0.192  TRUE       TRUE               TRUE    
# ℹ 1 more variable: sso_match <lgl>

$coefficient provides detail for each coefficient and is useful for data visualization.

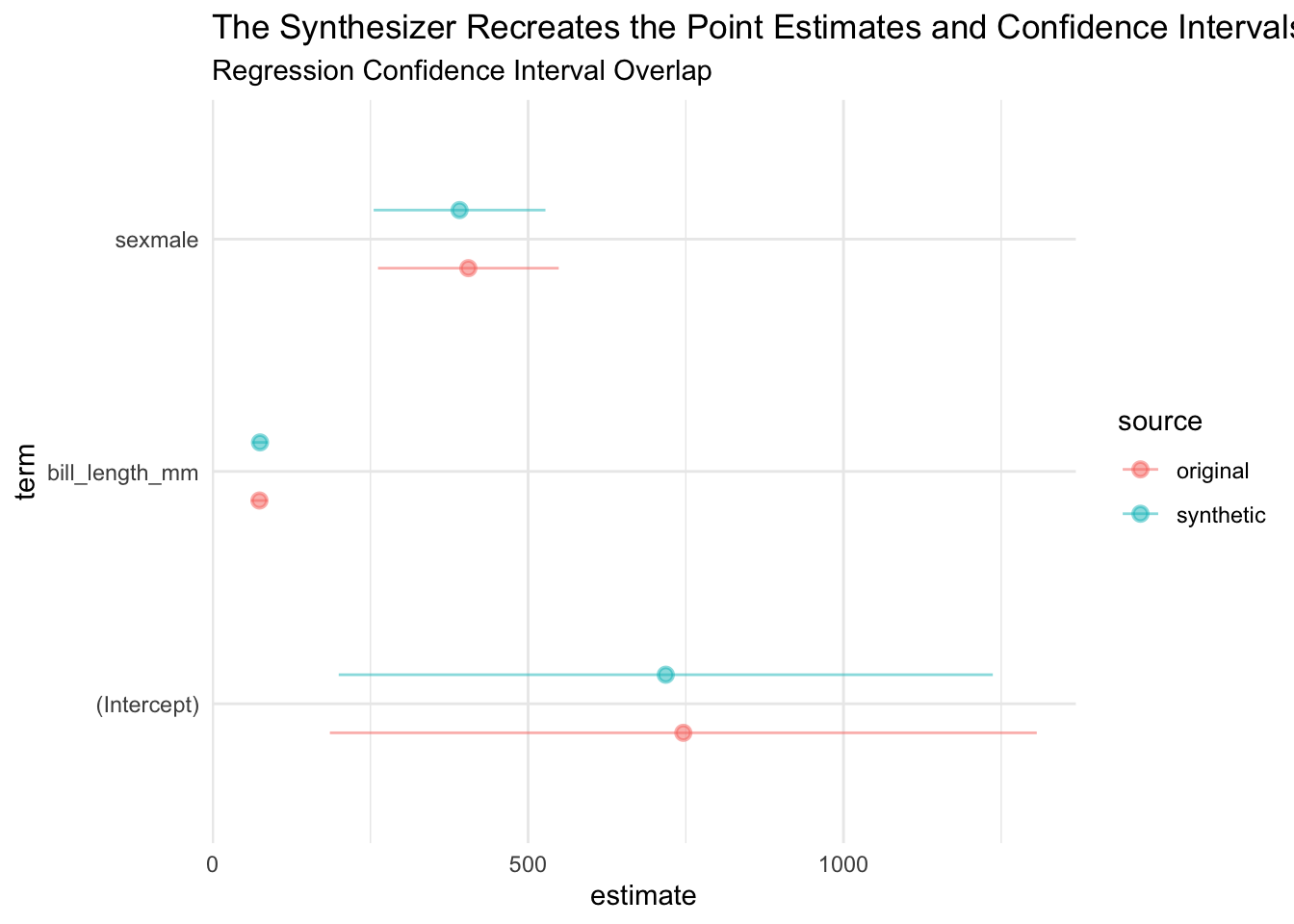
ci_overlap$coefficient |>
  ggplot(aes(x = estimate, xmin = conf.low, xmax = conf.high, y = term, color = source)) +
  geom_pointrange(alpha = 0.5, position = position_dodge(width = 0.5)) +
  labs(
    title = "The Synthesizer Recreates the Point Estimates and Confidence Intervals",
    subtitle = "Regression Confidence Interval Overlap"
  )

6.1.9 Discriminant-Based Metrics

Discriminant-based metrics build models to predict if an observation is original or synthetic and then evaluate those model predictions. Ideally, it should be difficult for a model to distinguish, or discriminate, between original observations and synthetic observations.

  • Any classification model that generates probabilities from library(tidymodels) can be used to generate propensities (the estimated probability than observation is synthetic).
  • By default, the code creates a training/testing split and returns separate metrics for each split. This can be turned off with split = FALSE.
  • The code can handle hyperparameter tuning.
  • After calculating propensities, the code can calculate ROC AUC, SPECKS, pMSE, and pMSE ratio.

6.1.9.1 Example Using Decision Trees

Discriminant-based metrics are built a discrimination object created by discrimination().

disc1 <- discrimination(postsynth = penguins_postsynth, data = penguins_conf)

Next, we use library(tidymodels) to specify a model. We recommend the tidymodels tutorial to learn more.

library(tidymodels)

rpart_rec <- recipe(
  .source_label ~ ., 
  data = disc1$combined_data
)

rpart_mod <- decision_tree(cost_complexity = 0.01) %>%
  set_mode(mode = "classification") %>%
  set_engine(engine = "rpart")

Next, we fit the model to the data to generate predicted probabilities.

disc1 <- disc1 %>%
  add_propensities(
    recipe = rpart_rec,
    spec = rpart_mod
  )

At this point, we can use

  • add_discriminator_auc() to add the ROC AUC for the predicted probabilities
  • add_specks() to add SPECKS for the predicted probabilities
  • add_pmse() to add pMSE for the predicted probabilities
  • add_pmse_ratio(times = 25) to add the pMSE ratio using the pMSE model and 25 bootstrap samples
disc1 %>%
  add_discriminator_auc() %>%
  add_specks() %>%
  add_pmse() %>%
  add_pmse_ratio(times = 25)
$combined_data
# A tibble: 666 × 8
   .source_label species island    sex    bill_length_mm bill_depth_mm
   <fct>         <fct>   <fct>     <fct>           <dbl>         <dbl>
 1 original      Adelie  Torgersen male             39.1          18.7
 2 original      Adelie  Torgersen female           39.5          17.4
 3 original      Adelie  Torgersen female           40.3          18  
 4 original      Adelie  Torgersen female           36.7          19.3
 5 original      Adelie  Torgersen male             39.3          20.6
 6 original      Adelie  Torgersen female           38.9          17.8
 7 original      Adelie  Torgersen male             39.2          19.6
 8 original      Adelie  Torgersen female           41.1          17.6
 9 original      Adelie  Torgersen male             38.6          21.2
10 original      Adelie  Torgersen male             34.6          21.1
# ℹ 656 more rows
# ℹ 2 more variables: flipper_length_mm <dbl>, body_mass_g <dbl>

$propensities
# A tibble: 666 × 10
   .pred_synthetic .source_label .sample  species island    sex   bill_length_mm
             <dbl> <fct>         <chr>    <fct>   <fct>     <fct>          <dbl>
 1           0.290 original      testing  Adelie  Torgersen male            39.1
 2           0.290 original      training Adelie  Torgersen fema…           39.5
 3           0.290 original      training Adelie  Torgersen fema…           40.3
 4           0.636 original      testing  Adelie  Torgersen fema…           36.7
 5           0.290 original      training Adelie  Torgersen male            39.3
 6           0.290 original      training Adelie  Torgersen fema…           38.9
 7           0.290 original      training Adelie  Torgersen male            39.2
 8           0.290 original      training Adelie  Torgersen fema…           41.1
 9           0.636 original      testing  Adelie  Torgersen male            38.6
10           0.8   original      training Adelie  Torgersen male            34.6
# ℹ 656 more rows
# ℹ 3 more variables: bill_depth_mm <dbl>, flipper_length_mm <dbl>,
#   body_mass_g <dbl>

$discriminator
══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: decision_tree()

── Preprocessor ────────────────────────────────────────────────────────────────
0 Recipe Steps

── Model ───────────────────────────────────────────────────────────────────────
n= 498 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

  1) root 498 249 synthetic (0.50000000 0.50000000)  
    2) bill_length_mm< 38.75 117  47 synthetic (0.59829060 0.40170940)  
      4) body_mass_g>=4000 15   3 synthetic (0.80000000 0.20000000) *
      5) body_mass_g< 4000 102  44 synthetic (0.56862745 0.43137255)  
       10) bill_depth_mm< 17.85 62  21 synthetic (0.66129032 0.33870968) *
       11) bill_depth_mm>=17.85 40  17 original (0.42500000 0.57500000)  
         22) bill_length_mm< 34.8 8   2 synthetic (0.75000000 0.25000000) *
         23) bill_length_mm>=34.8 32  11 original (0.34375000 0.65625000)  
           46) island=Torgersen 11   4 synthetic (0.63636364 0.36363636) *
           47) island=Biscoe,Dream 21   4 original (0.19047619 0.80952381) *
    3) bill_length_mm>=38.75 381 179 original (0.46981627 0.53018373)  
      6) island=Biscoe,Dream 350 170 original (0.48571429 0.51428571)  
       12) species=Chinstrap 108  49 synthetic (0.54629630 0.45370370)  
         24) bill_length_mm< 49.15 66  23 synthetic (0.65151515 0.34848485)  
           48) sex=male 18   1 synthetic (0.94444444 0.05555556) *
           49) sex=female 48  22 synthetic (0.54166667 0.45833333)  
             98) bill_length_mm< 45.35 22   6 synthetic (0.72727273 0.27272727) *
             99) bill_length_mm>=45.35 26  10 original (0.38461538 0.61538462) *
         25) bill_length_mm>=49.15 42  16 original (0.38095238 0.61904762) *
       13) species=Adelie,Gentoo 242 111 original (0.45867769 0.54132231)  
         26) bill_length_mm>=51.2 27  10 synthetic (0.62962963 0.37037037)  
           52) flipper_length_mm< 226.5 16   3 synthetic (0.81250000 0.18750000) *
           53) flipper_length_mm>=226.5 11   4 original (0.36363636 0.63636364) *
         27) bill_length_mm< 51.2 215  94 original (0.43720930 0.56279070)  
           54) bill_depth_mm>=19.05 26  11 synthetic (0.57692308 0.42307692)  
            108) body_mass_g< 3962.5 13   2 synthetic (0.84615385 0.15384615) *
            109) body_mass_g>=3962.5 13   4 original (0.30769231 0.69230769) *
           55) bill_depth_mm< 19.05 189  79 original (0.41798942 0.58201058) *
      7) island=Torgersen 31   9 original (0.29032258 0.70967742) *

$discriminator_auc
# A tibble: 2 × 4
  .sample  .metric .estimator .estimate
  <fct>    <chr>   <chr>          <dbl>
1 training roc_auc binary         0.700
2 testing  roc_auc binary         0.475

$pmse
# A tibble: 2 × 4
  .source   .pmse .null_pmse .pmse_ratio
  <fct>     <dbl>      <dbl>       <dbl>
1 training 0.0356     0.0317       1.12 
2 testing  0.0318     0.0320       0.995

$specks
# A tibble: 2 × 2
  .source  .specks
  <fct>      <dbl>
1 training  0.325 
2 testing   0.0595

attr(,"class")
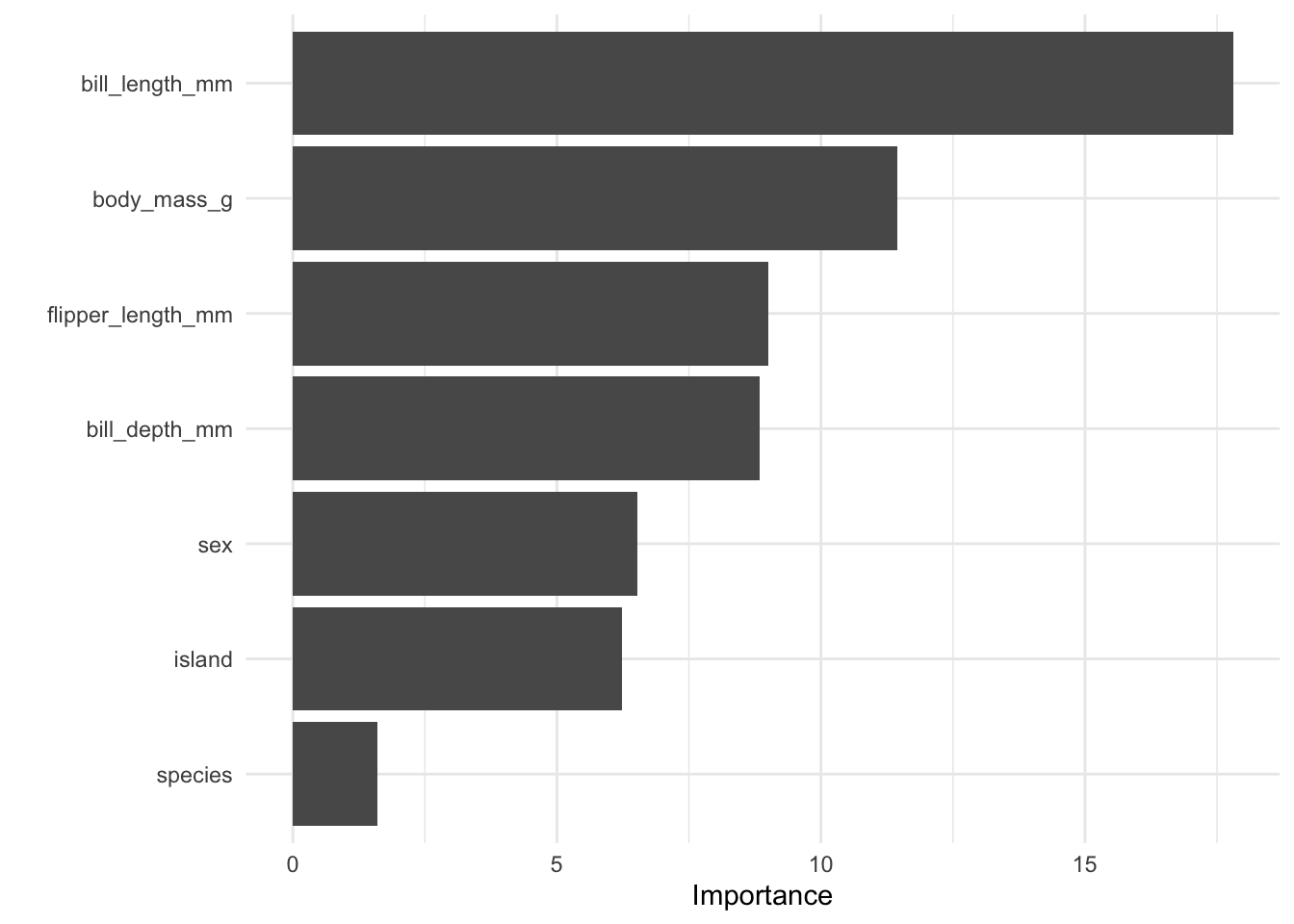
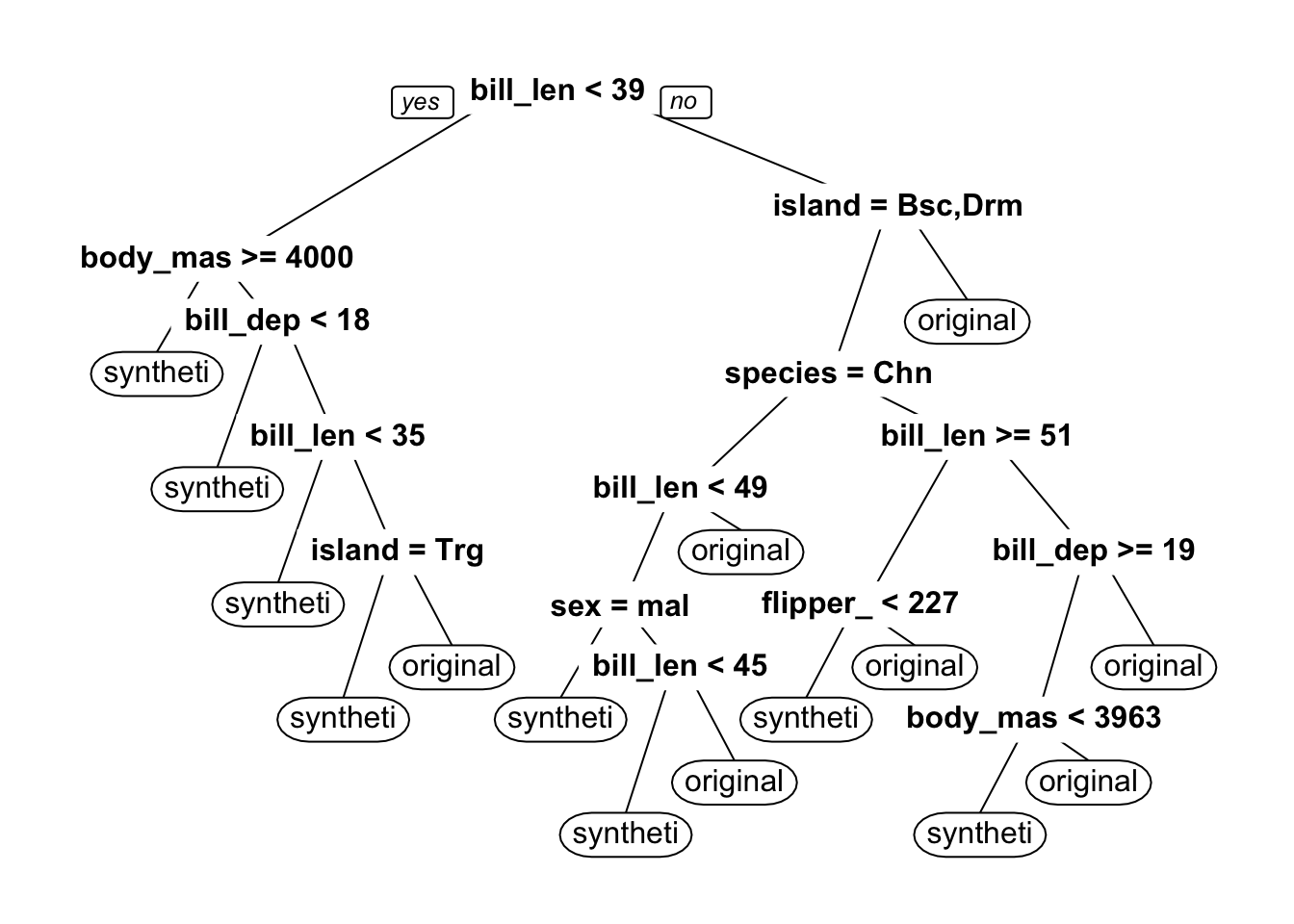
[1] "discrimination"

Finally, we can look at variable importance and the decision tree from our discriminator.

library(vip)
library(rpart.plot)
disc1$discriminator %>% 
  extract_fit_parsnip() %>% 
  vip()

disc1$discriminator$fit$fit$fit %>%
  prp()

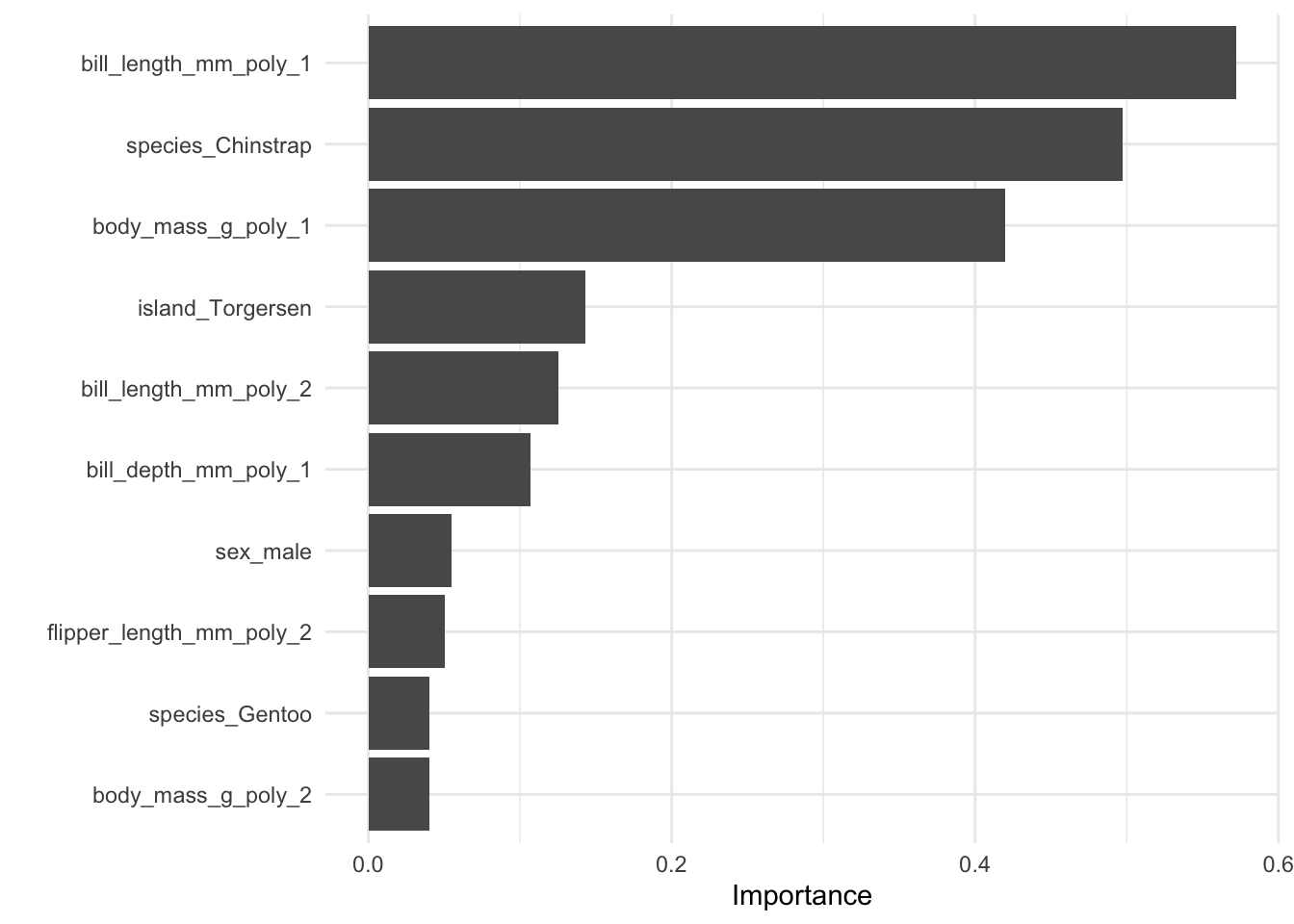
6.1.9.2 Example Using Regularized Regression

Let’s repeat the workflow from above with LASSO logistic regression and hyperparameter tuning.

# create discrimination
disc2 <- discrimination(postsynth = penguins_postsynth, data = penguins_conf)

# create a recipe that includes 2nd-degree polynomials, dummy variables, and
# standardization
lasso_rec <- recipe(
  .source_label ~ ., 
  data = disc2$combined_data
) %>%
  step_poly(all_numeric_predictors(), degree = 2) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_normalize(all_predictors())

# create the model
lasso_mod <- logistic_reg(
  penalty = tune(), 
  mixture = 1
) %>%
  set_engine(engine = "glmnet") %>%
  set_mode(mode = "classification")

# create a tuning grid
lasso_grid <- grid_regular(penalty(), levels = 10)

# add the propensities
disc2 <- disc2 %>%
  add_propensities_tuned(
    recipe = lasso_rec,
    spec = lasso_mod,
    grid = lasso_grid
  ) 
# calculate metrics
disc2 %>%
  add_discriminator_auc() %>%
  add_specks() %>%
  add_pmse() %>%
  add_pmse_ratio(times = 25)
$combined_data
# A tibble: 666 × 8
   .source_label species island    sex    bill_length_mm bill_depth_mm
   <fct>         <fct>   <fct>     <fct>           <dbl>         <dbl>
 1 original      Adelie  Torgersen male             39.1          18.7
 2 original      Adelie  Torgersen female           39.5          17.4
 3 original      Adelie  Torgersen female           40.3          18  
 4 original      Adelie  Torgersen female           36.7          19.3
 5 original      Adelie  Torgersen male             39.3          20.6
 6 original      Adelie  Torgersen female           38.9          17.8
 7 original      Adelie  Torgersen male             39.2          19.6
 8 original      Adelie  Torgersen female           41.1          17.6
 9 original      Adelie  Torgersen male             38.6          21.2
10 original      Adelie  Torgersen male             34.6          21.1
# ℹ 656 more rows
# ℹ 2 more variables: flipper_length_mm <dbl>, body_mass_g <dbl>

$propensities
# A tibble: 666 × 10
   .pred_synthetic .source_label .sample  species island    sex   bill_length_mm
             <dbl> <fct>         <chr>    <fct>   <fct>     <fct>          <dbl>
 1           0.410 original      training Adelie  Torgersen male            39.1
 2           0.432 original      training Adelie  Torgersen fema…           39.5
 3           0.325 original      training Adelie  Torgersen fema…           40.3
 4           0.453 original      training Adelie  Torgersen fema…           36.7
 5           0.340 original      training Adelie  Torgersen male            39.3
 6           0.444 original      testing  Adelie  Torgersen fema…           38.9
 7           0.471 original      training Adelie  Torgersen male            39.2
 8           0.332 original      testing  Adelie  Torgersen fema…           41.1
 9           0.366 original      training Adelie  Torgersen male            38.6
10           0.585 original      testing  Adelie  Torgersen male            34.6
# ℹ 656 more rows
# ℹ 3 more variables: bill_depth_mm <dbl>, flipper_length_mm <dbl>,
#   body_mass_g <dbl>

$discriminator
══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
3 Recipe Steps

• step_poly()
• step_dummy()
• step_normalize()

── Model ───────────────────────────────────────────────────────────────────────

Call:  glmnet::glmnet(x = maybe_matrix(x), y = y, family = "binomial",      alpha = ~1) 

   Df %Dev    Lambda
1   0 0.00 0.0309100
2   3 0.06 0.0281700
3   4 0.16 0.0256600
4   5 0.34 0.0233800
5   4 0.51 0.0213100
6   6 0.66 0.0194100
7   8 0.80 0.0176900
8   8 0.92 0.0161200
9   8 1.02 0.0146900
10  8 1.11 0.0133800
11  8 1.18 0.0121900
12  8 1.24 0.0111100
13  9 1.40 0.0101200
14 10 1.58 0.0092230
15 10 1.73 0.0084040
16 10 1.85 0.0076570
17 10 1.95 0.0069770
18 10 2.04 0.0063570
19 10 2.11 0.0057920
20 10 2.17 0.0052780
21 10 2.22 0.0048090
22 10 2.26 0.0043820
23 10 2.30 0.0039920
24 10 2.33 0.0036380
25 10 2.35 0.0033150
26 10 2.37 0.0030200
27 10 2.39 0.0027520
28 10 2.40 0.0025070
29 10 2.41 0.0022850
30 11 2.42 0.0020820
31 11 2.43 0.0018970
32 11 2.44 0.0017280
33 11 2.45 0.0015750
34 12 2.45 0.0014350
35 12 2.46 0.0013070
36 12 2.46 0.0011910
37 12 2.47 0.0010850
38 12 2.47 0.0009890
39 13 2.47 0.0009011
40 13 2.48 0.0008211
41 13 2.48 0.0007481
42 13 2.48 0.0006817
43 13 2.48 0.0006211
44 13 2.49 0.0005659
45 13 2.49 0.0005156
46 13 2.49 0.0004698

...
and 1 more lines.

$discriminator_auc
# A tibble: 2 × 4
  .sample  .metric .estimator .estimate
  <fct>    <chr>   <chr>          <dbl>
1 training roc_auc binary         0.599
2 testing  roc_auc binary         0.439

$pmse
# A tibble: 2 × 4
  .source    .pmse .null_pmse .pmse_ratio
  <fct>      <dbl>      <dbl>       <dbl>
1 training 0.00798    0.00689        1.16
2 testing  0.00880    0.00691        1.27

$specks
# A tibble: 2 × 2
  .source  .specks
  <fct>      <dbl>
1 training   0.201
2 testing    0.155

attr(,"class")
[1] "discrimination"
# look at variable importance
library(vip)

disc2$discriminator %>% 
  extract_fit_parsnip() %>% 
  vip()

6.2 Additional Functionality

6.2.1 Grouping

Many utility metrics include a group_by argument to group the metrics by group during calculation. For example, this code calculates moments by species.

util_moments(
  postsynth = penguins_postsynth, 
  data = penguins_conf,
  group_by = species
)
# A tibble: 60 × 7
   species   variable       statistic original synthetic difference
   <fct>     <fct>          <fct>        <dbl>     <dbl>      <dbl>
 1 Adelie    bill_length_mm count      146       153          7    
 2 Chinstrap bill_length_mm count       68        78         10    
 3 Gentoo    bill_length_mm count      119       102        -17    
 4 Adelie    bill_length_mm mean        38.8      38.5       -0.294
 5 Chinstrap bill_length_mm mean        48.8      47.3       -1.56 
 6 Gentoo    bill_length_mm mean        47.6      48.0        0.475
 7 Adelie    bill_length_mm sd           2.66      2.93       0.267
 8 Chinstrap bill_length_mm sd           3.34      3.07      -0.273
 9 Gentoo    bill_length_mm sd           3.11      3.40       0.299
10 Adelie    bill_length_mm skewness     0.156     0.505      0.349
# ℹ 50 more rows
# ℹ 1 more variable: proportion_difference <dbl>

6.2.2 Weighting

Many utility metrics include a weight_var argument to use weighted statistics during calculation. For example, this code weights the moments by the body weight of the penguins.

util_moments(
  postsynth = penguins_postsynth, 
  data = penguins_conf,
  weight_var = body_mass_g
)
# A tibble: 20 × 6
   variable        statistic original synthetic difference proportion_difference
   <fct>           <fct>        <dbl>     <dbl>      <dbl>                 <dbl>
 1 bill_length_mm  count      1.40e+6   1.39e+6   -1.5 e+4              -0.0107 
 2 bill_length_mm  mean       4.46e+1   4.41e+1   -4.71e-1              -0.0106 
 3 bill_length_mm  sd         5.38e+0   5.54e+0    1.60e-1               0.0297 
 4 bill_length_mm  skewness  -7.39e-2  -5.74e-2    1.64e-2              -0.222  
 5 bill_length_mm  kurtosis  -7.89e-1  -9.15e-1   -1.26e-1               0.160  
 6 bill_depth_mm   count      1.40e+6   1.39e+6   -1.5 e+4              -0.0107 
 7 bill_depth_mm   mean       1.70e+1   1.71e+1    1.28e-1               0.00754
 8 bill_depth_mm   sd         2.01e+0   1.94e+0   -7.07e-2              -0.0351 
 9 bill_depth_mm   skewness   1.05e-2  -1.37e-1   -1.47e-1             -14.0    
10 bill_depth_mm   kurtosis  -1.00e+0  -9.17e-1    8.70e-2              -0.0867 
11 flipper_length… count      1.40e+6   1.39e+6   -1.5 e+4              -0.0107 
12 flipper_length… mean       2.03e+2   2.01e+2   -1.97e+0              -0.00970
13 flipper_length… sd         1.44e+1   1.46e+1    1.60e-1               0.0111 
14 flipper_length… skewness   1.48e-1   3.99e-1    2.51e-1               1.70   
15 flipper_length… kurtosis  -1.14e+0  -1.04e+0    1.08e-1              -0.0940 
16 body_mass_g     count      1.40e+6   1.39e+6   -1.5 e+4              -0.0107 
17 body_mass_g     mean       4.36e+3   4.31e+3   -5.19e+1              -0.0119 
18 body_mass_g     sd         8.26e+2   8.17e+2   -9.84e+0              -0.0119 
19 body_mass_g     skewness   2.69e-1   4.64e-1    1.95e-1               0.724  
20 body_mass_g     kurtosis  -9.70e-1  -7.26e-1    2.44e-1              -0.251

Most commonly, weight_var is used when synthesizing data from surveys.

Horst, Allison Marie, Alison Presmanes Hill, and Kristen B Gorman. 2020. Palmerpenguins: Palmer Archipelago (Antarctica) Penguin Data. https://doi.org/10.5281/zenodo.3960218.